I was playing around with addition of fractions the other day and I thought that fractions could be added in such a way that the first fraction is normally presented, as a/c, whereas the second fraction, b/d, is considered as a multiple of itself and the “bit left over”, or (1 – a/c)b/d
Seriously it’s time for a bit of algebra !
If we have the “whole” as 1 then the special addition, “plus with a ring”, is defined as
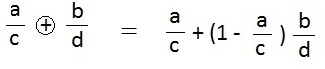
or as a diagram ———
Some simple algebraic examples will also show this.
The operation also produces a proper fraction for any two proper fractions.
Now the “plus with a ring” addition can be seen as a commutative operation.
See that the a/c and the b/d can be switched with no effect on the order of the two terms.
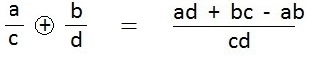
If that is not obvious the following rearrangement is clear indeed.
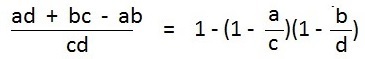
I calculated the two arrangements of the associative rule and it was also satisfied.
Do this yourselves !
Saving school math 