Comments 100and 101

10100-101100-101Elaine 1-11-15 fraction discussion between Howard and Elaine contd0-101

Division of Fractions, the logical approach

I have done the fraction stuff in “paint” as a picture, so it cant be edited. It was easier !

 

Order of Operations, from Wikipedia

This article spells it out:

https://en.wikipedia.org/wiki/Order_of_operations

The surprise is the amazing variation within the computer applications.

 

Proportional Addition of Fractions

I was playing around with addition of fractions the other day and I thought that fractions could be added in such a way that the first fraction is normally presented, as a/c, whereas the second fraction, b/d, is considered as a multiple of itself and the “bit left over”, or (1 – a/c)b/d

Seriously it’s time for a bit of algebra !

If we have the “whole” as 1 then the special addition, “plus with a ring”, is defined as

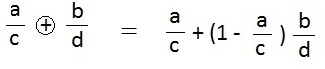
or as a diagram ———

Some simple algebraic examples will also show this.

The operation also produces a proper fraction for any two proper fractions.

Now the “plus with a ring” addition can be seen as a commutative operation.
See that the a/c and the b/d can be switched with no effect on the order of the two terms.

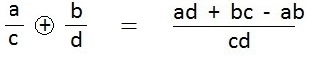
If that is not obvious the following rearrangement is clear indeed.

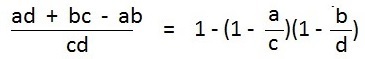
I calculated the two arrangements of the associative rule and it was also satisfied.

Do this yourselves !

Subtraction using addition

 

subtraction with adding

4531
3726
====
add 3 to both items. 6 and 3 makes 9
4534
3729
====
add 70 to both items. 70 and 20 makes 90
4604
3799
====
add 200 to both items. 700 and 200 makes 900
4804
3999
====
====
result 804 + 1 = 805

Subtraction and Negative Numbers : Part_2

Using the and connective.

In “apple words” we have
start with 7 apples
subtract 3 apples
result 4 apples

or as a single “sentence”,
Starting with 7 apples and subtracting 3 apples gives the result 4 apples
or without the apples,
Start with 7 and subtract 3, gives the result 4

Using the minus sign in place of subtract.

We can simply replace subtract by minus in the “subtract 3 apples” expression as they have the same meaning.

And we can use the minus sign, ” − “, instead of the word.

So we have converted subtract into the minus sign, and, correspondingly, add into the plus sign, ” + “, and used the word and to link the terms together.

Beginning with the example on the previous post,

start with 9, add 2, subtract 3, subtract 5, add 4, subtract 2 (final state 5)

we get the expression on the left

(start with) 9 and +2 and -3 and -5 and +4 and -2

and since the and connectives are all of the connectives we can dispense with them and write the expression as

(start with) 9  +2  −3  −5  +4  −2 with result or final state 5

We can even cross out the start with at the beginning as it is always there,

and simplify using the arithmetical equals, or ” = ” :

9  +2  −3  −5  +4  −2 = 5

Multiplication and division, with numbers.

An example:

start with 5, add 6, multiply by 4, multiply by 2, subtract 21, result is 32

5 and +6, multby 4, multby 2, and -21

5 +6*4*2 -21 result 32

At this point there appears to be a problem:

Do we multiply out the factors, (multbys), before the sums are calculated, or afterwards?

The convention is to multiply the factors in each group of multbys first, and then combine (and) the add and subtract items.

For the above calculation the result develops as follows:

5 +6*4*2 -21 = 32
5 +6*8 -21 = 32
5 +48 -21 = 32
=32

And with two groups of mults:
5 +6*3 +1 -2*4 +12 = 28
5 +18 +1 -2*4 +12 = 28
5 +18 +1 -8 +12 = 28
= 28

And now we have to do ALGEBRA.

Algebra – expressions, terms and factors.

A term in algebra is not just a number, preceded by a “+” or a “−”, it is a number (which may be 1 and can be ignored) followed if needed by a sequence of letters (variables) and expressions. Each of the expressions is enclosed in brackets (parentheses).

An algebraic expression is (startwith) 0, followed by a list of terms.

Simple example :

(startwith) 0 +8a +bx

The (startwith) number is always zero and we can ignore it, leaving only the terms.

The first  term has a “+” or a “−”, and we can ignore the first “+”, as 8a +bx

If the terms are rearranged then the missing “+” needs to be put back in,
as in bx +8a

Examples:

8a +bx
4 +3x −7xy
-4 +3x −7xy
and with included expressions like (x +5):
4 +3x(x +5)
2 -5x -6(x +2)(x +9)

The value of an expression is the numerical result of the expression when all the individual variables are replaced by numbers and combined.

An equation is two expressions with an “equals” sign between them.

If the value of the left side of an equation is equal to the value of the right side then the equation is satisfied. The number on the left equals the number on the right.

Examples:

x +3 = 4x -6

The equation is satisfied when x = 3, and nowhere else.

3x -a = 2x where x = 6. Now find “a” to satisfy the equation.

The distributive property of multiplication over addition. 

This is the most important feature of arithmetic and algebra, where the additive form of an expression is converted into a multiplicative form, and vice versa.

Four examples will show the methods:

a(x +y) = ax +ay

ax +bx = (a +b)x

(a +b)(x +y) = ax +ay +bx +by

(a −b)(x −y) = ax −ay −bx +by

This last is a bit obscure, but a two dimensional array will help.

More tricky details, for  exponents and for division in algebra.

Exponents: Simple examples

2 +3x²  +3^x

5 +4x +6^{x +2}

The two examples above are the conventional forms of expressions with exponents.

The two below are fully bracketed expressions showing the linked pairs of parentheses, and showing the signs and numbers for the exponents. “^” is the sign for “exponent”.

2 +(3 *(x ^2)) +(3 ^x))

5 +(4 *x) +(6 ^(x +2))

These are both one-line expressions.

Division: Simple  examples

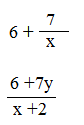
The two examples above are the conventional forms of expressions with division.

The two below are fully bracketed expressions showing the linked pairs of parentheses, and showing the signs and numbers for division. “/” is the sign for “divide by”.

6 +(7 /x)
(6 +(7 *y)) /(x +2)

These are also both one-line expressions.

——————————————————————————————————————————

It will appear that with the “apple” construction the formulae for arithmetic and algebra are identical.

 

Subtraction – what exactly is it? Part 1 (bonus: code for minus is 8722)

Addition

I had 5 apples, and then my brother gave m  2 more apples.
I now have 7 apples.

The process is

Without the pictures: 
Starting state (5 apples)
Action (add 2 apples)(and bunch them up !)
Final state (7 apples)

With a single sentence or equation, with the result
Start with 5, add 2, and resulting state is 7

Or the equation with apples
Start with 5 apples, add 2 more apples, and result is 7 apples

Subtraction

I have 7 apples now, and then my brother takes 3 of them away.
I end up with 4 apples .

The process is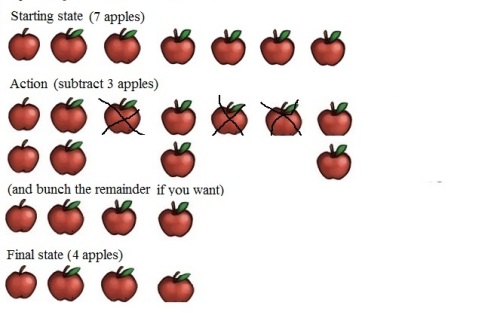

Without the pictures:
Starting state (7 apples)
Action (subtract 3 apples)
Final state (4 apples)

With a single sentence or equation, and the result
Start with 7, subtract 3, and resulting state is 4

Or the equation with apples
Start with 7 apples, subtract 3 apples, and result is 4 apples

Both of these equations are read from left to right

— – – – – – – – – – – – – –  – – – – – – – – – – – – – – – – – – – – – – – – – – –  – – – –  — – 

Counting and adding.

If I start with 1 and then add 1 I get 2. This doesn’t seem to be a problem at all.

If I start with 2 and then add 1 I get 3. This doesn’t seem to be too big a problem.

If I start with 5 and then add 3 I get 8. This  starts to get interesting because starting with 2 and adding 5 has exactly the same final state.

It is all to do with counting.

If I count a pile of bricks and there are ten of them I can jumble the bricks around and count them again. I will still have ten of them. The count is “how many” and nothing else.

Consequently the rearrangement has no counting effect, and so any collection of numbers with plus signs and a total of ten can be rearranged, to give the same total of ten.

For example:

start 2, add 3, add 4, add 1 is the same total as start 2, add 4, add 1, add 3 (result ten)

We can also swap the start number and the add number with an example:

start 3, add 5 is start 4, add 4 and then start 5, add 3. Same total.

And finally, with add we can combine two adds to get add 3, add 2 = add 5

Counting and subtracting.

The apple example:

Starting state (7 apples)
Action (subtract 3 apples)
Final state (4 apples)

The starting state, or start number, is 7
The action is subtract 3
and the final state is 4

— – – – – – – – – – – – – –  – – – – – – – – – – – – – – – – – – – – – – – – – – –  – – – –  — – 

 Subtracting several numbers.

Have a look at the following:

9 and −2 and −4

The final state is 3, but so is  9 and −4 and −2

Consequently the two subtractions can be swapped.

It’s even better than this: The adds and the subtracts can be put in any order, with the same final state.

Try
start with 9, add 2, subtract 3, subtract 5, add 4, subtract 2 (final state 5)
or rearranged
start with 9, add 2, add 4, subtract 3, subtract 5, subtract 2 (final state 5)

— – – – – – – – – – – – – –  – – – – – – – – – – – – – – – – – – – – – – – – – – –  – – – –  — – 

Properties of operations – a critique

Operations and Algebraic Thinking, CCSS grade 1 (italics)
Represent and solve problems involving addition and subtraction.
1. ………
2. ………Understand and apply properties of operations and the relationship
between addition and subtraction.
3. Apply properties of operations as strategies to add and subtract.
Examples:
If 8 + 3 = 11 is known, then 3 + 8 = 11 is also known. (Commutative property of
addition.) To add 2 + 6 + 4, the second two numbers can be added to make
a ten, so 2 + 6 + 4 = 2 + 10 = 12. (Associative property of addition.)

In mathematics there are numerous algebraic structures each consisting of a set of elements equipped with an operation that combines any two elements to form a third element. (Wikipedia, adapted, 19th century math)

So we can find an example of this where any two elements in the set of natural numbers can be combined with “+”, with the usual interpretation. (7 + 4 = 11).

More specifically we can use the “commutative property” of addition, a feature of the natural number system, to tell us that 7 + 4 equals 4 + 7 , for example.

BUT take a look at the above example, with different numbers:
7 − 6 + 4
Swap 4 and 6
7 − 4+ 6
So we have to avoid the negative operator.

The conclusion is that the commutative rule applies only when all the operators are plus operators.

Now what are we going to make of this ?????????

Table 3. The properties of operations. Here a, b and c stand for arbitrary numbers in a given number system. The properties of operations apply to the rational number system, the real number system, and the complex number system. (CCSS)
Commutative property of addition is a+ b = b + a

This is a definition. It states that “a complicated name” is what we know already, and can actually prove by counting. So it is a complete waste of time for K-7 or further.

Not only that, but the actions add 3 and subtract 4 are the original 17th and 18th century statements, and are proper algebra.

wiggly line

The Chain Rule and the Theory

I FOUND THIS ACCOUNT OF THE CHAIN RULE FROM SAM SHAH
https://samjshah.com/2018/02/08/there-might-be-light-at-the-end-of-the-chain-rule-tunnel-maybe/

The partial text is as follows:

Find two points close to each other, like (x,g(f(x)) and (x+0.001,g(f(x+0.001)).
Find the slope between those two points: {g(f(x+0.001)-g(f(x))}/{(x+0.001)-x}.
There we go. An approximation for the derivative! (We can use limits to write the exact expression for the derivative if we want.)

But that doesn’t help us understand that {d/dx}[g(f(x)]=g'(f(x))f'(x) on any level. They seem disconnected!

But I’m on my way there. I’m following things in this way: x >>> f >>> g

Check out this thing I whipped up after school today. The diagram on top does x >>> f and the diagram on the bottom does f >>> g. The diagram on the right does both. It shows how two initial inputs (in this case, 3 and 3.001) change as they go through the functions f and g.
At the very bottom, you see the heart of this.

It has {δg}/{δf} times {δf}/{δx}={δg}/{δx}

(END OF SAM SHAH’S BIT)

Proof of the chain rule.
We can be more exact and use the derivatives, and show that the formula is true for Y = G(F(X)) with F(X) = X ^N and G(F) = F ^M
The direct solution for Y’ is the derivative of X ^MN, that is MNX ^{MN – 1}
The formula solution is MF ^{M – 1} times NX ^{N – 1}, giving MNX ^N(M-1) times X ^N-1
and finally MNX ^{MN – 1}

SOME DEFINITIONS:
A function is a process which converts an input into a corresponding output.
In symbols, input –> f –> output

Examples:
The input is transformed (converted) into the output,
usually by a formula or an expression using the values of the input:
output = 2(input) + 5
or you can write this as output = 2 times input + 5

The input and the output are both expressions, which can be
a: a number, or
b: a single variable, x or y or z … , or
c: a more complicated expression

The commonest form for the input-output relationship for a function f
is, as an example, f(x) = 3x + 4, where x is an input
and the corresponding output is 3x + 4
f is the label of the function,
and f(x) is the expression whose value is 3x + 4
f(x) = 3x + 4 is then an equation
The equation can be seen for example as f(8) = 3 x 8 + 4,
or f(y) =3y + 4 using y as the input,
or f(z² + 5z + 7) = 3(z² + 5z + 7) + 4 using an expression.

In its most simple formulation the input is not present and the equation is simply f = 3y +4, where the input
is identified as the ‘y’.
Now if an equation has a single variable on the left and an expression on the right then
a) it can be interpreted as a function (functional form) with f(y) = 3y + 4, and
b) the expression on the right can be substituted for the variable on the left.

Example
Let g(A) = A + 2 be a function g with output A + 2
Then it can be identified with the equation g = A + 2
Let g have the input x² – 4x + 3
Then the output is (x + 2)² – 4(x + 2)x + 3
which is x² – 1 (surprise, surprise)

The Chain Rule and the theory.

I found this account of the chain rule from Sam Shah

https://samjshah.com/2018/02/08/there-might-be-light-at-the-end-of-the-chain-rule-tunnel-maybe/

The partial text is as follows:

Find two points close to each other, like (x,g(f(x)) and (x+0.001,g(f(x+0.001)).
Find the slope between those two points: {g(f(x+0.001)-g(f(x))}/{(x+0.001)-x}.
There we go. An approximation for the derivative! (We can use limits to write the exact expression for the derivative if we want.)

But that doesn’t help us understand that {d/dx}[g(f(x)]=g'(f(x))f'(x) on any level. They seem disconnected!

But I’m on my way there. I’m following things in this way: x >>> f >>> g

Check out this thing I whipped up after school today. The diagram on top does x \rightarrow f and the diagram on the bottom does f \rightarrow g. The diagram on the right does both. It shows how two initial inputs (in this case, 3 and 3.001) change as they go through the functions f and g.
At the very bottom, you see the heart of this.

It has {δg}/{δf} times {δf}/{δx}={δg}/{δx}

(end of Sam Shah’s bit)
We can be more exact and use the derivatives, and show that the formula is true for y = g(f(x)) with f(x) = x ⁿ and g(f) = f ^m
The direct solution for y’ is the derivative of x ^mn, that is mnx ^{mn – 1}
The formula solution is mf ^{m – 1} times nx ^{n – 1}, giving mnx ^n(m-1) times x ^n-1
and finally mnx ^{mn – 1}

 

SOME DEFINITIONS:
A function is a process which converts an input into a corresponding output.
In symbols, input –> f –> output

Examples:
The input is transformed (converted) into the output,
usually by a formula or an expression using the values of the input:
output = 2(input) + 5
or you can write this as output = 2 x input + 5

The input and the output are both expressions, which can be
a: a number, or
b: a single variable, x or y or z … , or
c: a more complicated expression

The commonest form for the input-output relationship for a function f
is, as an example, f(x) = 3x + 4, where x is an input
and the corresponding output is 3x + 4

f is the label of the function,
and f(x) is the expression whose value is 3x + 4
f(x) = 3x + 4 is then an equation
The equation can be seen for example as f(8) = 3 x 8 + 4,
or f(y) =3y + 4 using y as the input,
or f(z² + 5z + 7) = 3(z² + 5z + 7) + 4 using an expression.

In its most simple formulation the input is not present and the equation is simply f = 3y +4, where the input
is identified as the ‘y’.

Now if an equation has a single variable on the left and an expression on the right then
a) it can be interpreted as a function (functional form) with f(y) = 3y + 4, and
b) the expression on the right can be substituted for the variable on the left.
Example
Let g(A) = A + 2 be a function g with output A + 2
Then it can be identified with the equation g = A + 2
Let g have the input x² – 4x + 3
Then the output is (x + 2)² – 4(x + 2)x + 3
which is x² – 1 (surprise, surprise)