Not more CCSSM horrors, just some glaring omissions.

Glaring omissions to me, that is.

The obsession with Al Gebra and manipulations has used up loads of time which could have been spent on

1. Parameters.
The sudden appearance of the word “parameter” in High School :
“Interpret expressions for functions in terms of the situation they model. 5. Interpret the parameters in a linear or exponential function in terms of a context.”
The idea of a parameter is basic to the study of functions and relationships. At the start the equation y = mx + b has four letters in it. x and y are variables. What on earth are m and b? Numbers? Fixed numbers? Variable numbers, but not as variable as variables? No, they are parameters for the line. For a given line they are fixed, but for different lines one or both are different.
(When I was at school we, that is the kids, used to call them “variable constants”)

2. Parametric representation of curves and relationships.
For example a circle. With parameter θ a point (x,y) on the unit circle is described by x = cos(θ), y = sin(θ)
and a parabola, parameter a, point on curve given by x = a, y = a²
and for a lot of curves the only neat way.
It also allows for ease in programming graphics of curves.

3. Polar coordinates. The ONLY mention of the word “polar” is with regard to representation of complex numbers. With no way of simple plotting them ?????
How about the function representation of a circle as r = 2 ??

There are others!

It was admitted at the time of development of the CCSSM that too much time was spent on K-8, and HS math was a rough job – so why can it not be modified ???????
 

Halving a triangle, follow-up number two, pursuing the hyperbola

Halving the triangle, any triangle, led to the equation XY = 2 as the condition on the points on two sides of the triangle, distant X and Y from the vertex.
The envelope of this set of lines turned out to be a hyperbola.
But XY = 2 defines a hyperbola – what is the connection ?

I took xy = 1 for the condition, on a standard xy grid, and wrote it as representing a function x —-> y, namely y = 1/x
The two points of interest are then (x,0) on the x-axis and (0,1/x) on the y-axis.
We need the equation of the line joining these two points, so first of all we have to see that our x, above, is telling us which line we are talking about, and so it is a parameter for the line.
We had better give it a different name, say p.
Now we can find the equation of the line in x,y form, using (p,0) and (0,1/p) for the two points:
(y – 0)/(1/p – 0) = (x – p)/(0 – p)
which is easier to read as yp = -x/p + 1, and easier to process as yp² = -x + p

Now comes the fun bit !
To find the envelope of a set of straight lines we have to find the points of intersection of adjacent lines (really? adjacent?). To do this we have to find the partial derivative (derivative treating almost everything as constant) of the line equation with respect to the parameter p. A later post will reveal all about this mystifying procedure).
So do it and get  2yp = 1

And then eliminate p from the two equations, the line one and the derived one:
From the derived equation we get p = 1/(2y), so substituting in the line equation gives 1 = 2xy
This is the equation of the envelope, and written in functional form it is
y = 1/(2x), or (1/2)(1/x)
Yes ! Another rectangular hyperbola, with the same asymptotes.
(write it as xy = 1/2 if you like)

Now I thought “What will this process do with y = x² ?”
So off I go, and to cut a long story short I found the following:
For y = x² the envelope was y = (-1/4)x², also a multiple of the original, with factor -1/4

Some surprise at this point, so I did it for 1/x² and for x³
Similar results: Same function, with different factors.
Try it yourself ! ! ! ! ! ! !

This was too much ! No stopping ! Must find the general case ! (y = x^k)
Skipping the now familiar details (left to the reader, in time honoured fashion) I found the following:

Original equation: y = x^k

Equation of envelope: y = x^k multiplied by -(k-1)^k-1/k^k

which I did think was quite neat.
—————————————————————
The next post will be the last follow-up to the triangle halving.

—————————————————————
Constructions made with GEOSTRUCT, an online browser application:

To get geostruct from the net click
http://www.mathcomesalive.com/geostruct/geostructforbrowser1.html

and to download the .doc instructions file
http://www.mathcomesalive.com/geostruct/geostruct basics.doc

Halving a triangle, follow-up number one, ellipse

The previous post is “Analytic (coordinate) geometry has its good points, but elegance is not one of them”, in which a formula for any line cutting a triangle in half was found. The envelope of the cutting line for one section (of three) of the triangle was found to be always a hyperbola, which got me thinking “How do I get an ellipse?”. Clearly not by cutting a triangle in half, which involved taking two points A’ and B’on adjacent sides of the triangle, and making the product of their distances from the point of intersection of the sides equal to half the product of the lengths of the two sides.

So we cannot take two distances along two lines from the same point, lets try two distances from separate points on two lines, and keep the product of the distances constant. Magic:

The base line is AF. Line DL is set parallel to AF. B and G are the two points of interest, where AB and DG are the two distances, and the envelope of the line BG is an ellipse which touches AF and DL. The really interesting thing about this is that the lines do not have to be parallel, and that as the points A and F are placed nearer and nearer to the point of intersection the ellipse becomes more and more hyperbolic at the nearby end.

The next post will be a different follow-up to the triangle halving.

Constructions made with GEOSTRUCT, an online browser application:

To get geostruct from the net click
http://www.mathcomesalive.com/geostruct/geostructforbrowser1.html

and to download the .doc instructions file
http://www.mathcomesalive.com/geostruct/geostruct basics.doc

 

More on √2 – Common Crappiness Simply Seen (CCSS)

It’s strange how one can read something many times and miss the complete stupidity of it, in math at any rate.
This is from the CCSSM Grade 8:
The Number System 8.NS (Grade 8)
Know that there are numbers that are not rational, and approximate
them by rational numbers.
2. Use rational approximations of irrational numbers to compare the size
of irrational numbers, locate them approximately on a number line
diagram, and estimate the value of expressions (e.g., π²). For example,
by truncating the decimal expansion of √2, show that √2 is between 1 and
2, then between 1.4 and 1.5, and explain how to continue on to get better
approximations.

I need an approximation to √2. Just get me the decimal expansion, please. Oh, and I need it to 73 decimal places.

Do I have to explain to the authors of this garbage that the only way I am going to get anywhere with √2 is by a process of successive approximation, NOT THE OTHER WAY ROUND ! !

And just try doing this for pi.

“I know that there are irrational numbers”. “How do you know that?”. “Because my teacher told me”.

And where will I encounter π² ? Or “estimate the value of pi-e”.

And when we get to High School we find:

Use properties of rational and irrational numbers.
3. Explain why the sum or product of two rational numbers is rational;
that the sum of a rational number and an irrational number is irrational;
and that the product of a nonzero rational number and an irrational
number is irrational.

I find real difficulties explaining the last point.

I am not proposing that we go as far as Cauchy Sequences or Dedekind cuts, but if they cannot do a better job than this the topic is best stopped at “√2 is irrational and here’s why”. How many students can prove that √2+√3 is irrational?

Analytic (coordinate) geometry has its good points, but elegance is not one of them.

This all started with a post by Maya Quinn (mathwater.wordpress.com) on problem solving. An oblong piece has been removed from an oblong cake (why? who did that?).The problem was to cut the remainder of the cake into two equal parts. Lots of solutions, one in particular was very imaginative.
This led me to another problem – what if the cut-out piece was triangular?

In view of one of the solutions to the first problem I decided that the triangle should be chopped in half. Not as simple as chopping a rectangle in half !

So, with Polya at my side (he’s been there since 1962) I decided that an equilateral triangle would be a reasonable starting point, as at least it was obvious that there were a few lines through the centroid doing the job (the medians), so some generality was still around.
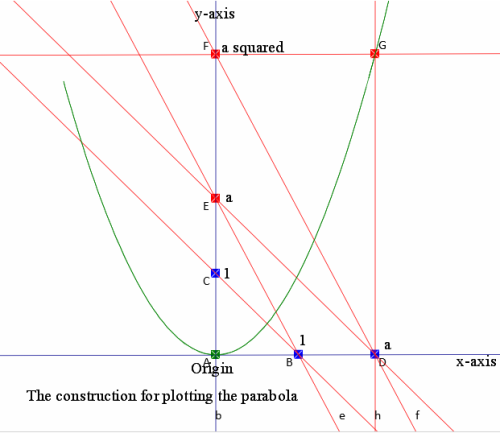
Here is the equilateral triangle, nicely resting on the x axis, side length 2, top point on the y axis.

The vertical median bisects the triangle, so I described the general bisector GH by the distances x=DG and y=EH

In order to find out more about the bisector lines I first found a relationship between x and y, which was y=2x/(1+x), based on the area calculations:

Height of equilateral triangle is √3, base is 2, so area is √3

Height of BGH triangle is (2-y)/2 * √3, base is 1+x, so area is (1/2)*(1+x)*(2-y)/2*√3

and this is to be half of √3

So (1/2)*(1+x)*(2-y) must be equal to 1, and this leads to  y=2x/(1+x)
This allowed me to find the coordinates of the point H and locate it correctly on the line.

I then joined the points and by moving G the line moved, and I tracked it, shown in green below.

Small notational irritation: In the diagram below G is now C and H is now K

The visible curve is called the envelope of the lines, and it (obviously) touches the medians.

The complete envelope of the bisecting lines consists of two more sections, making a “concave”triangle with the centroid in the middle.

At this point I figured that a change of variable was in order, and looking at the y=2x/(1+x) equation, and at the diagram it looked like the distances of the two points from the left hand vertex would be helpful:

This produced X=1+x and Y=2-y, and to my surprise the resulting equation was Y=2/X, or XY=2.

The significance of this last equation escaped me at this point.

So I found the coordinates of the two points C and K in a coordinate system with origin at point A, in terms of the new variables X and Y, found the line joining them, rewrote in terms of a parameter P, used a bit of calculus to get the envelope (I’ll do a post on this later), and it had the second degree equation

√3/4 = y² – √3y – √3xy + 3x

which is a hyperbola !!! (see C. Smith “Conic Sections”)

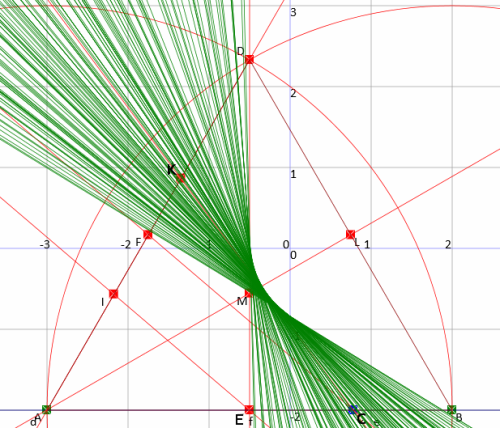
At this point I stopped thinking about halving a triangle, and looked at the full envelope for one of the three sections, and got this:

A complete hyperbola, and, not only that, its asymptotes appear to be sides of the equilateral triangle. (Which when you think about it is not completely unreasonable !).

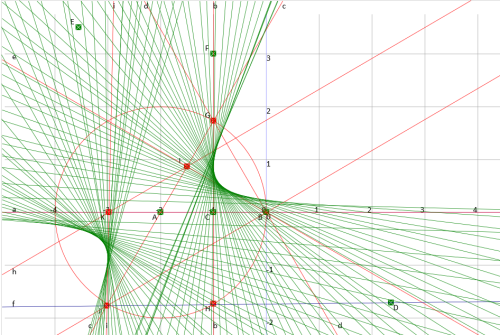
Then, thinking about doing shear operations on the picture, and with the X, Y variables, and ratios of lengths of segments on the same line being unchanged, I constructed the whole lot on an arbitrary triangle and did the envelope:

The triangle is ADF and the halving line is BG. Yes ! Same result !

At which point I saw a bit of light, and thought that “XY=2” does not involve angles at all.

Ooops, there’s  another formula for the area of a triangle: a*b*sin(C)/2

Then straightaway all was revealed. You can draw the picture !
1. Triangle ACB, point X on side AC, point Y on side BC, area=0.5*AC*BC*sin(ACB)
2. Triangle XCY, area 0.5*XC*YC*sin(XCY), but angles ACB and XCY are the same, so if we require the area of triangle XCY to be half the area of triangle ACB we get 0.5*XC*YC*sin(XCY)=0.5*0.5*AC*BC*sin(ACB)

which reduces to (XC/AC)*(YC/BC)=0.5, and this does not involve the angle.

This corresponds to our earlier XY=2 since the equilateral triangle had side length 2

Pure speculation suggests that this result may have some connection with the way that the angle bisector of an angle in a triangle divides the opposite side in the ratio of the two adjacent sides.
———————————————–
The geometric diagrams were all constructed with the web based program
http://www.mathcomesalive.com/geostruct/geostructforbrowser1.html
√3

What is a number? Particularly √2

After the previous post, on the reality or otherwise of the square root of -1, I thought that the square root of 2 might benefit from a similar inquiry. After all, what can we actually say about √2 ? The answer to this question is very simple. “Not a lot !”.

In the real world of engineering, architecture, mathematical modelling, business, medicine and so on numbers are either counts (1,2,3,4,…) or absolute or relative measurements (1.20cm, 240 secs, 15 mins, 4096 ft, 35.7 mph,….). The first group is the natural or counting numbers, the second group is the rational numbers, and not so many of them. In practice it is rare for the size of a quantity to be expressed with more than four significant figures. So every practical quantity has a measurement in the form of a rational number, and most importantly IT CAN BE WRITTEN DOWN. I am going to call this the VALUE of the number.

The only thing is an assertion that there is a sort of number which when multiplied by itself produces the value 2.

So where does that leave √2 ?  It cannot be written down in the form of a rational number, so it has NO value in the above sense.
Ok, I can write  1.4142² < 2 < 1.4143² but neither of the two values shown is the value of √2. I could go on and get more digits in the two numbers and this would still be true.

This all started with the ancient Greeks, who found out that the length of the diagonal of a unit square was a quantity very different from quantities which could be measured using the side length of a unit square as the measurement unit. They described this state of affairs as “The side length and the diagonal length of a square are incommensurable”, which is a nice long word.

In passing I have to say that the Common Core math makes a real pig’s ear of this stuff.

So the Greeks were happy with the idea that every line segment has a length, and that the length is expressed as a number, but this wasn’t good enough for the nineteenth century mathematicians. I may write about this later, but for now we should be seeing if √2 can reasonably be “joined ” to the rational number system in a non magical, non wishful thinking way.

Let’s pretend that √2 is a sort of number, and that new numbers can be formed by a rational number “a” plus a rational amount “b” of √2, and write this as a + b√2

Then the sum of two these comes in as
(a + b√2) + (p + q√2) = (a + p) + (b + q)√2

and the product comes in as 
(a + b√2)(p + q√2) = (ap + 2bq) + (aq + bp)√2

In each case we have another of the “new” numbers.

One tricky question remains. What about division ?

If I multiply a + b√2 by a – b√2 I get a² – 2b² which has no √2 in it, it is a normal rational number, and it is only zero if BOTH a and b are zero.
This is called the root(2) conjugate.
In a division, if the divisor has its b not zero then I can multiply the top and the bottom (the divisor and the dividend) by the conjugate of the bottom, and the only √2’s are then on top.

(3+2√2)/(4-√2) = (3+2√2)(4+√2)/((4-√2)(4+√2)) = (16+11√2)/(16-2) …

As with the square root of -1 we can see that this is all about pairs of rational numbers, and the √2 symbol just keeps the members of each pair in order.

So rewriting the multiplication we get (a,b)(p,q) = (ap + 2bq, aq + bp)
and all the rules for operations can be expressed in this way and be seen to work.

We have ended up with a totally valid extension of the rational numbers by √2.
It is quite amusing to represent these pairs on an xy grid, and see the effect of multiplication.

But √2 still does not have a value ! ! ! ! !
 

The square root of minus one asked me “Do I exist?”

Complex number.
“complex” as opposed to “simple” ?
“number” for what ?
Not for counting !
Not for measuring ! We’ll see about that !
“Square root of -1”, maybe, if that means anything at all !

Who needs the “i” ? It’s not essential.
Here goes…..

They say that (a+ib)(p+iq) = ap – bq + (bp + aq)i
But only if i is the square root of -1.

Getting rid of the i
Let us put the a and the b in a+ib together in brackets, as (a,b), and call this “thing” a “pair”.
This gets rid of the (magic) i straightaway.

Let us define an operation * to combine pairs:
(a,b)*(p,q) = (ap-bq, bp+aq)
This is the “pair” version of the “multiplication of complex numbers”.

It’s more interesting to read this as “(a,b) is applied to (p,q)”, and even better if we think of (p,q) as a “variable” and “apply (a,b)” as a function.
Ok, so we will write (x,y) instead of (p,q), and then
(a,b)*(x,y) = (ax-by, bx+ay)
Let us call the output of the “apply (a,b)” function the pair (X,Y)
Then
X = ax-by
Y = bx+ay
Now we can see this as a transformation of points in the plane:
The function “apply (a,b)” sends the point (x,y) to the point (X,Y)

Looking at some simple points we see that
(1,0)*(x,y) = (x,y)….no change at all
(-1,0)*(x,y) = (-x,-y)…the “opposite” of (x,y),
so doing (-1,0)* again gets us back to no change at all.
(0,1)*(x,y) = (-y,x)….which you may recognize as a rotation through 90 deg.
and doing (0,1)* again we get
(0,1)*(0,1)*(x,y) = (0,1)*(-y,x) = (-x,-y)….a rotation through 180 deg.

So with a bit of faith we can see that (0,1)*(0,1) is the same as (-1,0), and also that (-1,0)*(-1,0) = (1,0)…check it!
Consequently we have a system in which there are three interesting operations:
(1,0)* has no effect, it is like multiplying by 1
(-1,0)* makes every thing negative, it is like multiplying by -1, and
(0,1)*(0,1)* has the same effect as (-1,0)*

So we have found something which behaves like the square root of -1, and it is expressed as a pair of ordinary numbers.
It is then quite reasonable to give the name “i” to this “thing”, and use “i squared = -1”.

And generally, a complex number can be seen as a pair of normal (real) numbers, and bye-bye the magic !

When you think about it a fraction also needs two numbers to describe it.

Next post : matrix representation of “apply (a,b) to (x,y)”.