Area models for completing the square, dynamic approach.

An area model, or a dot array model (same thing really) is one way of illustrating the algebraic completion of a square.

I have used dots as they are easier to create.

The quadratic is viewed initially as the “standard form”, and then rebuilt dynamically line by line into the “square plus a bit over” form, as shown in the following sequence:

The odd valued coefficient of x in the original expression can appear as a row and a column of half-dots, or half squares in the area model form.

Geometry and Numbers – the theory

 

Multiplication, the theory – by Thales’ theorem

The diagram can be simplified by using an acute triangle.

   Thales’ theorem

Proof of Thales theorem :
If a line is drawn parallel to one side of a triangle and it intersects the other two sides at two distinct points then it divides the two sides in the same ratio.
Given : In ∆ABC , DE || BC and intersects AB in D and AC in E.
Prove that : AD / DB = AE / EC
Construction : Join BC,CD and draw EF ┴ BA and DG ┴ CA.
Statements                                                    Reasons
1) EF ┴ BA                                                      1) Construction
2) EF is the height of ∆ADE and ∆DBE     2) Definition of perpendicular
3)Area(ADE) = (AD.EF)/2                             3)Area = (Base .height)/2
4)Area(DBE) =(DB.EF)/2                               4) Area = (Base .height)/2
5)(Area(ADE))/(Area(DBE)) = AD/DB         5) Divide (3) by (4)
6) (Area(ADE))/(Area(DEC)) = AE/EC         6) Divide (3) by Area(DEC)
7) ∆DBE ~∆DEC                                             7) Both the ∆s are on the same base and
between the same || lines.
8) Area(∆DBE)=area(∆DEC)                        8) So the two triangles have equal areas
9) AD/DB =AE/EC                                           9) From (5) and (6) and (7)

Not only this but also AD/AB = DE/BC

I borrowed this from http://www.ask-math.com/basic-proportionality-theorem.html

Some adjustments, but the Thales theorem is well done. I liked it.

Geometry and Numbers – negative ones – “a minus times a minus is a plus”

To accommodate positive and negative numbers we need two extended number lines, with their zeros at the same place

Then multiplication of two negative numbers will always give a positive result, following the same geometrical structure.

The start, where the multiplier begins at 1

Now the 1 connects with the multiplicand -3

The multiplier is now placed at -2

 6

And the parallel line from -2 connects to the 6 on the target line

This is so geometrical, and there is no “funny business”. None of the “ought to be 6”. No stuff about the distributive law.

The only geometry needs the Pythagoras theorem, and this will be the next post.

Geometry and Numbers, not the counting sort

A number line is generally a piece of straight line with a starting point, labeled 0, and equally spaced points labeled 1 and 2 and 3 and 4 and so on till the paper runs out.

The value of a number is the distance from the zero point to the numbered point, in units of the equal spacing.

It is really much easier to draw one of these !

Addition

Two parallel number lines, same scale.

Notice that the zero points do not have to be in the same vertical line.

Subtraction

To get the symbolic form 7 – 2 = 5 we start with 0 on the target line (now the upper line) and join it to the 2 on the subtrahend line. (arrow down) (needs a nicer word here)

Then from the 7 on the subtrahend line we produce the line from 7 parallel to the 0 to 2 line. Then “arrow up” to the target line

Magic ! The result is 5 on the target line.

I like the picture, but the subtraction words are a mess.

Multiplication

We need two number lines, but since multiplication is  “proportional” they will now be crossing, and the common point is labeled 0.

Also, the labels are “target” and “multiplier” and each line has its own scale.

 

Bonus: Nomograms, with lines.

The first is a simple calculator, with A + B = Sum

The second one calculates parallel resistances

 

 

Matrix inversion, row ops, program added

The row operation matrix inversion method is so neat and ingenious, and it has the same operations for all dimensions of matrix.

Here is a step by step approach, where firstly the dimension is chosen, then the first of the buttons is selected (Start). After which the buttons are selected in order. The states of the left and right matrices are displayed at each stage, and finally the identity matrix appears on the left, and the inverse of the original matrix appears on the right.

http://mathcomesalive.com/mathsite/matrix%20prog%203.html

The first display shows the original matrix on the left. Nothing has been done yet.

 

The second one is the 2 x 2 matrix inverted.

The third is the 4 x 4 matrix inverted.

The matrices can be altered with the file name for the application, “matrix prog 3.html”. using right click and “view page source”. You are then on your own, with javascript !!!!!!!!

Negative numbers, the minus sign, abstract algebra.

I was pondering the reality of negative numbers and after figuring out that a sequence of dots on a line can be extended in each of the two directions, and then arbitrarily selecting one dot as “the zero”. The line can be further labelled as 1, 2, 3, … to one side and -1, -2, -3, … on the other side.
(better to label the 1, 2, 3, … as +1, +2, +3, … and consider the lot as “signed numbers”)

Soon proceeding towards arithmetic I concluded that 7-3 is 4, and also 8-4 is 4, and therefore 13-9 is 4, and then 3-7 is -4, and -2-2 is -4. It was then observed that if a-b=c then a-y-(b-y) is also equal to c, regardless of the signs of the specific numbers involved.
This of course is stunningly obvious when looking at the signed difference of the first and the second number as an extended number line diagram.

The outcome of all this was an arithmetic for 0, 1, 2 modulo 3, and  the signed difference x-y is a binary operation diff(x,y) with table:

…x  … 0     1     2
y
0         0     1     2
1         2      0    1
2         1      2    0

Example: 1-2 is -1, which is 2 modulo 3

So a non abelian, non associative algebra with a not quite identity satisfies the conditions, where A=1, B=2 and C=0
—————————————————–
There are three objects and an operation called “doesn’t have a name”.
Two are similar, and the third is a bit different
They are paired to yield a single object as follows:

AA = BB = CC = C
AB = BC = CA = B
AC = CB = BA = A

Notice that BC and CB are different, so non-abelian.
Worse is that (AC)A = C and A(CA) = B are different, so non-associative.
And consequently A and B and C are different.
—————————————————-

Interestingly, and maybe separately, the minus sign behaves very differently from the plus sign:

a-(-b) is a+b, but there is no way of writing a-b using only addition.

This means that all expressions can be written with “minus” alone.

Scary, and not just mathematically speaking …

Try this for size:

https://mystudentvoices.com/how-old-is-the-shepherd-the-problem-that-shook-school-mathematics-ad89b565fff#.a7llwy3mv

Adding fractions – phew!

Who needs LCM ?

First, three views of LCM with no comments :

1: Change them to equivalent fractions that will have equal
denominators. As the common denominator, choose the LCM of
the original denominators. Then the larger the numerator, the
larger the fraction.

2: Jun 26, 2011 – If b and d were same it was easy to find LCM
since if denominators are same, we just need to find LCM of
numerators, hence LCM of (a/b) and (c/b) would be LCM(a,c)/b.
So we have to first make denominators of both the fractions same.
Multiply numerator and denominator of first fraction by LCM
(b,d)/b.

3: The GCF and LCM are the underlying concepts for finding
equivalent fractions and adding and subtracting fractions, which
students will do later.

 

Now we can do fraction addition without LCM. It just needs the use of the distributive law, and the result shows the way in which the divisors combine.

And now using 3/4

But the best one is via multiplication ……

Now for multiplication and division.

 

 

A minus times a minus is a plus -Are you sure you know why?

What exactly are negative numbers?
A reference , from Wikipedia:
In A.D. 1759, Francis Maseres, an English mathematician, wrote that negative numbers “darken the very whole doctrines of the equations and make dark of the things which are in their nature excessively obvious and simple”.
He came to the conclusion that negative numbers were nonsensical.[25]

A minus times a minus is a plus
Two minuses make a plus
Dividing by a negative, especially a negative fraction !!!!
(10 – 2) x (7 – 3) = 10 x 7 – 2 x 7 + 10 x -3 + 2 x 3, really? How do we know?
Or we use “the area model”, or some hand waving with the number line.

It’s time for some clear thinking about this stuff.

Mathematically speaking, the only place that requires troublesome calculations with negative numbers is in algebra, either in evaluation or in rearrangement, but what about the real world ?
Where in the real world does one encounter negative x negative ?
I found two situations, in electricity and in mechanics:

1: “volts x amps = watts”, as it it popularly remembered really means “voltage drop x current flowing = power”
It is sensible to choose a measurement system (scale) for each of these so that a current flowing from a higher to a lower potential point is treated as positive, as is the voltage drop.

Part of simple circuit A———–[resistors etc in here]————–B
Choosing point A, at potential a, as the reference, and point B, at potential b, as the “other” point, then the potential drop from A to B is a – b
If b<a then a current flows from A to B, and its value is positive, just as a – b is positive
If b>a then a current flows from B to A, and its value is negative, just as a – b is negative

In each case the formula for power, voltage drop x current flowing = power, must yield an unsigned number, as negative power is a nonsense. Power is an “amount”.
So when dealing with reality minus times minus is plus (in this case nosign at all).

The mechanics example is about the formula “force times distance = work done”
You can fill in the details.

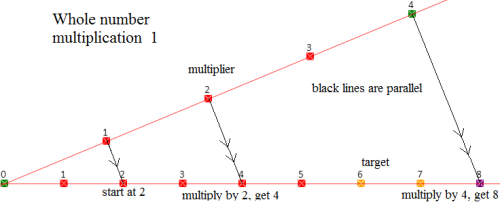
Now let’s do multiplication on the number line, or to be more precise, two number lines:
Draw two number lines, different directions, starting together at the zero. The scales do not have to be the same.
To multiply 2 by three (3 times 2):
1: Draw a line from the 1 on line A to the 2 on line B
2: Draw a line from the 3 on line A parallel to the first line.
3: It meets line B at the point 6
4: Done: 3 times 2 is 6

Number line A holds the multipliers, number line B holds the numbers being multiplied.

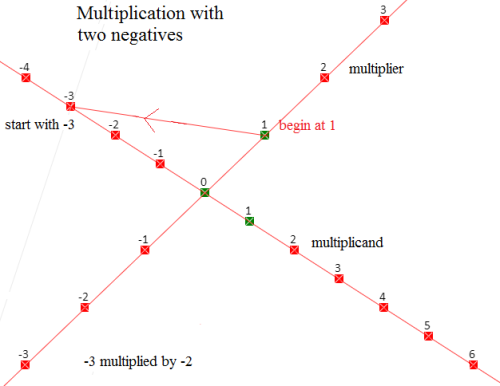
To multiply a negative number by a positive number we need a pair of signed number lines, crossing at their zero points.

So to multiply -2 by 3 (3 times -2) we do the same as above, but the number being multiplied is now -2, so 1 on line A is joined to -2 on line B

The diagram below is for -2 times 3. Wow, it ends in the same place.

Finally, and you can see where this is going, we do -2 times -3.

Join the 1 on line A to the -3 on line B, and then the parallel to this line passing through the -2 on line A:

and as hoped for, this line passes through the point 6 on the number line B.

Does this “prove” the general case? Only in the proverbial sense. The reason is that we do not have a proper definition of signed numbers. (There is one).

Incidentally, the numbering on the scales above is very poor. The positive numbers are NOT NOT NOT the same things as the unsigned numbers 1, 1.986, 234.5 etc

Each of them should have a + in front, but mathematicians are Lazy. More on this another day.

Problem for you: Show that (a-b)(c-d) = ac – bc – ad + bd without using anything to do with “negative numbers”

*******************************************

References.
Wikipedia:
Reference direction for current
Since the current in a wire or component can flow in either direction, when a variable I is defined to represent
that current, the direction representing positive current must be specified, usually by an arrow on the circuit
schematic diagram. This is called the reference direction of current I. If the current flows in the opposite
direction, the variable I has a negative value.

Yahoo Answers: Reference direction for potential difference
Best Answer: Potential difference can be negative. It depends on which direction you measure the voltage – e.g.
which way round you connect a voltmeter. (if this is the best answer, I hate to think of what the worst answer is)
********************************************

Plus ca change, plus c’est la meme chose

Apologies for no accents!

1: Khan Academy 2016 Subtraction to 1000 You don’t have to watch it all! Run it faster if possible.

2: Tom Lehrer (cover version) original from the 60’s The New Math