The Future

“How’s your Mary doing?”.

“She’s doing well. She’s 8 now. She’s in Grade 3. She really enjoys the Pre-Algebra and the Pre-Textual Analysis.”.

Smarter Balanced: Lacking Smarts; Precariously Balanced

It’s a bit long, but it sure takes the lid off the CCSS. Read it now.

deutsch29: Mercedes Schneider's Blog

In this time of  “public-education-targeted boldness,” the Common Core State Standards (CCSS) has made the American public one whopper of a “bold” promise:

The standards were created to ensure that all students graduate from high school with the skills and knowledge necessary to succeed in college, career, and life, regardless of where they live. [Emphasis added.]

There is neither now nor never has been any empirical investigation to substantiate this “bold” claim.

Indeed, CCSS has not been around long enough to have been thoroughly tested. Instead, the above statement–which amounts to little more than oft-repeated advertising– serves as its own evidence.

However, if it’s on the *official* CCSS website, and if CCSS proponents repeat it constantly, that must make it true… right?

Keep clicking your heels, Dorothy.

Now, it is one issue to declare that CCSS works. It is quite another to attempt to anchor CCSS assessments to the above cotton…

View original post 1,321 more words

The View from Japan: Common Core is a Disaster in the Making

Observations about high stakes testing from an American teacher who is teaching in a University in Japan.

Creative by Nature

 “What many supporters of Common Core ignore is that the “rigorous” high-stakes testing approach that they wish to impose on our children has been experimented with in many other nations, and has been a complete failure. Once in place it dominates all instruction, turning schools into test prep factories, and students into test-taking machines.”

I’m a full-time University teacher, living and working in Japan since 1994.  We had our entrance exams a few weeks ago, and part of the job for University teachers here is to mark certain sections of the tests by hand. One of the things I notice each year is that most Japanese students get 30 to 50% of the answers wrong.

Sometimes answers are close but test markers are looking for the “exact” right answer. If the student spells a word wrong they may receive half credit or no points. Why are we so strict with spelling? Because these kinds of high-stakes tests are designed to select and sort…

View original post 1,339 more words

Complex Numbers via Rigid Motions

https://howardat58.files.wordpress.com/2015/02/complex-numbers-by-rotations.doc

Complex numbers via rigid motions
Just a bit mathematical !

I wrote this in response to a post by Michael Pershan:
http://rationalexpressions.blogspot.com/2015/02/could-this-introduce-kids-to-complex.html?

The way I have presented it is showing how mathematicians think. Get an idea, try it out, if it appears to work then attempt to produce a logical and mathematically sound derivation.
(This last part I have not included)
The idea is that wherever you have operations on things, and one operation can be followed by another of the same type, then you can consider the combinations of the operations separately from the things being operated on. The result is a new type of algebra, in this case the algebra of rotations.
Read on . . .

Rotations around the origin.
angle 180 deg or pi
Y = -y, and X = -x —> coordinate transformation
so (1,0) goes to (-1,0) and (-1,0) goes to (1,0)
Let us call this transformation H (for a half turn)

angle 90 deg or pi/2
Y = x, and X = -y
so (1,0) goes to (0,1) and (-1,0) goes to (0,-1)
and (0,1) goes to (-1,0) and (0,-1) goes to (1,0)
Let us call this transformation Q (for a quarter turn)

Then H(x,y) = (-x,-y)
and Q(x,y) = (-y,x)

Applying H twice we have H(H(x,y)) = (x,y) and if we are bold we can write HH(x,y) = (x,y)
and then HH = I, where I is the identity or do nothing transformation.
In the same way we find QQ = H

Now I is like multiplying the coodinates by 1
and H is like multiplying the coordinates by -1
This is not too outrageous, as a dilation can be seen as a multiplication of the coordinates by a number <> 1

So, continuing into uncharted territory,
we have H squared = 1 (fits with (-1)*(-1) = 1
and Q squared = -1 (fits with QQ = H, at least)

So what is Q ?
Let us suppose that it is some sort of a number, definitely not a normal one,
and let its value be called k.
What we can be fairly sure of is that k does not multiply each of the coordinates.
This appears to be meaningful only for the normal numbers.

Now the “number” k describes a rotation of 90, so we would expect that the square root of k to describe a rotation of 45

At this point it helps if the reader is familiar with extending the rational numbers by the introduction of the square root of 2 (a surd, although this jargon seems to have disappeared).

Let us assume that sqrt(k) is a simple combination of a normal number and a multiple of k:
sqrt(k) = a + bk
Then k = sqr(a) + sqr(b)*sqr(k) + 2abk, and sqr(k) = -1
which gives k = sqr(a)-sqr(b) + 2abk and then (2ab-1)k = sqr(a) – sqr(b)

From this, since k is not a normal number, 2ab = 1 and sqr(a) = sqr(b)
which gives a = b and then a = b = 1/root(2)

Now we have a “number” representing a 45 degree rotation. namely
(1/root(2)*(1 + k)

If we plot this and the other rotation numbers as points on a coordinate axis grid with ordinary numbers horizontally and k numbers vertically we see that all the points are on the unit circle, at positions corresponding to the rotation angles they describe.

OMG there must be something in this ! ! !

The continuation is left to the reader (as in some Victorian novels)

ps. root() and sqrt() are square root functions, and sqr() is the squaring function .

pps. Diagrams may be drawn at your leisure !

Another Common Core Math Horror

I thought I had found them all, but NO.

Subtraction. Read this
————-
Kindergarten
Operations and Algebraic Thinking
• Understand addition as putting together and adding to, and understand subtraction as taking apart and taking from.
————-
What has subtraction got to do with taking apart ???
(The examples are all of the form 9 = 3 + 6 and so on).

Also there is NO mention at all of subtraction as a way of finding the difference between two numbers, or of finding the larger of two numbers (anywhere).

While I am in critical mode I offer two more, less awful, horrors from Grade 1:

“To add 2 + 6 + 4,…”  and  “For example, subtract 10 – 8″.

The poor symbols are clearly in great pain at this point. Just read aloud exactly what is written…..

Memorization versus Number Sense

This is a link to a post by WatsonMath about Stanford Professor Jo Boaler and her thoughts, opinions and research backed statements of the counterproductive combination of “learn your tables” and “take this (yet another !) timed test on them”.

Definitely worth reading, and worth passing on as well.

http://www.watsonmath.com/2015/02/07/jo-boaler-fluency-without-fear/

Interesting geometry result, again

To show that the angle bisector of an angle in a triangle splits the opposite side in the ratio of the two adjacent sides.

My first proof used angles in the same segment. See

Interesting geometry result

Several tries later (today) and i came up with this annoyingly simple proof: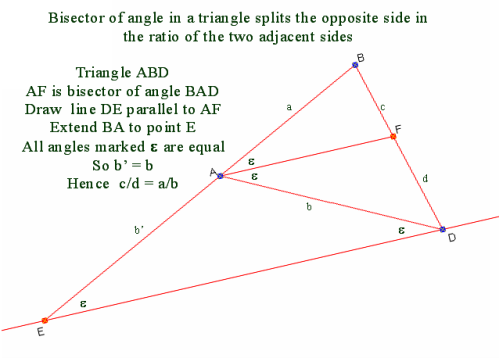

SOLVING PROBLEMS THAT MATTER, NOT GIVING ANSWERS

This is not mine, so read the original at

Solving Problems that Matter

I used to not give answers to my engineering students. They hated me ! When i pointed out that if they ever got hired it would be because the firm had problems to be solved, and they DIDN’T have the answers.

Math is Really Weird: On Strange Sums and Counterintuitive Results

The latest bit of weird math is going the rounds. Here is boxingpythagoras’s presentation of:
“So, now we’ve arrived at the strangest result of the day: S=1+2+3+4+5+6+…=-\frac{1}{12}”. (or -1/12)
together with comments from Joseph Nebus and myself.

Boxing Pythagoras

Whenever you add a finite integer to another finite integer, you always get a sum which is, itself, a finite integer. This, by itself, is not very shocking. When you add 1 to 1, you get 2. When you add 5 and -9, you get -4. When you add 0 and 299,792,458, you get 299,792,458. This is all rather unsurprising.

However, math can get weird once you start adding up an infinite collection of numbers. Take Zeno’s Dichotomy Paradox, for example. Numerically, we can represent this problem as an infinite summation: $latex S=sumlimits _{n=1}^infty frac{1}{2^n}=frac{1}{2}+frac{1}{4}+frac{1}{8}+frac{1}{16}+…+frac{1}{2^n}+…$ Even though we are adding up an infinite quantity of numbers, we arrive at a finite value– in this case, $latex S=1$. Arguably the most famous philosopher in history, Aristotle, would have vehemently objected to this formulation– and, in fact, did object rather loudly in his book Physics, when discussing this particular paradox. However…

View original post 1,255 more words

Commutative, distributive, illustrative-ly

Here they all are, apart from associative, as it belongs to algebra.